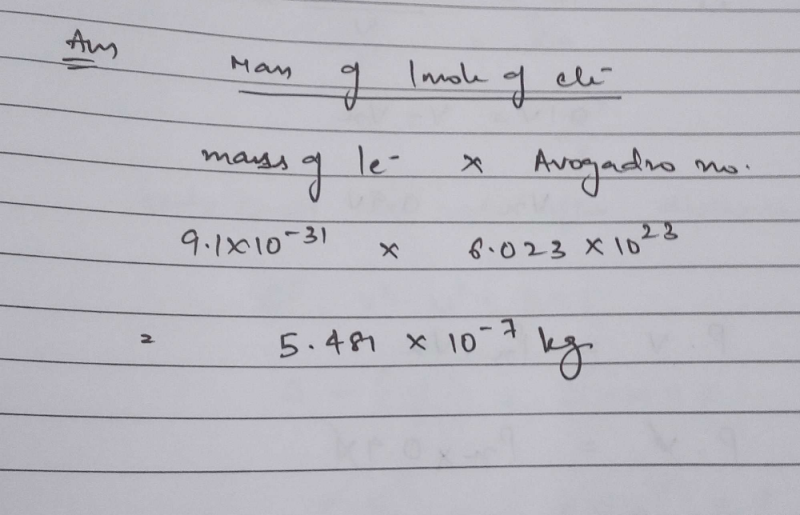How many electrons in ONE MOLE of carbon dioxide?
To calculate the mass of a single atom, first look up the atomic mass of carbon from the periodic table. This number, 12.01, is the mass in grams of one mole of carbon. One mole of carbon is 6.022 x 10 23 atoms of carbon (Avogadro's number). 4 8 × 1 0 − 7 K g; 9. 6 5 × 1 0 4 C One mole of electrons corresponds to 6. 0 2 3 × 1 0 2 3 electrons. Mass of one electron is 9. 1 × 1 0 − 3 1 kg.
3 Answers
Explanation:
first calculate the moles of
= 2.27 mol
now number of electrons in
= 22
thus one mole of
Explanation:
The first thing to do here is to calculate the number of moles of carbon dioxide present in your sample. To do that, use the compound's molar mass
Next, use Avogadro's constant to figure out the number of molecules of carbon dioxide present in the sample.
Now, every molecule of carbon dioxide contains
- one atom of carbon,
#1 xx 'C'# - two atoms of oxygen,
#2 xx 'O'#
This means that your sample contains
and
Next, grab a periodic Table and look for the atomic numbers of the two elements. You will find
As you know, a neutral atom has equal numbers of protons located inside its nucleus and electrons surrounding the nucleus.
Therefore, you can say that every atom of carbon will contain
This means that you will have
Mass Of 1 Mole Of Electron Microscope
which gets you
The answer must be rounded to one significant figure, the number of sig figs you have for the mass of carbon dioxide.
Explanation:
First, we calculate the number of electrons in ONE MOLECULE of
And then we calculate the number of carbon dioxide molecules in a mass of
And (finally) we solve the product:
Related questions
| General | |
|---|---|
| Symbol | 4He |
| Names | helium-4, He-4 |
| Protons | 2 |
| Neutrons | 2 |
| Nuclide data | |
| Natural abundance | 99.999863% |
| Half-life | stable |
| Isotope mass | 4.002603254 u |
| Spin | 0 |
| Binding energy | 28295.7 keV |
| Isotopes of helium Complete table of nuclides | |
Helium-4 (4
He
) is a stable isotope of the element helium. It is by far the more abundant of the two naturally occurring isotopes of helium, making up about 99.99986% of the helium on Earth. Its nucleus is identical to an alpha particle, and consists of two protons and two neutrons.
Alpha decay of heavy elements in the Earth's crust is the source of most naturally occurring helium-4 on Earth, produced after the planet cooled and solidified. While it is also produced by nuclear fusion in stars, most helium-4 in the Sun and in the universe is thought to have been produced by the Big Bang, and is referred to as 'primordial helium'. However, primordial helium-4 is largely absent from the Earth, having escaped during the high-temperature phase of Earth's formation.
Helium-4 makes up about one quarter of the ordinary matter in the universe by mass, with almost all of the rest being hydrogen.
When liquid helium-4 is cooled to below 2.17 kelvins (−271.17 °C), it becomes a superfluid, with properties that are very unlike those of an ordinary liquid. For example, if superfluid helium-4 is kept in an open vessel, a thin film will climb up the sides of the vessel and overflow. In this state and situation, it is called a 'Rollin film'. This strange behavior is a result of the Clausius–Clapeyron relation and cannot be explained by the current model of classical mechanics, nor by nuclear or electrical models – it can only be understood as a quantum-mechanical phenomenon. The total spin of the helium-4 nucleus is an integer (zero), and therefore it is a boson (as are neutral atoms of helium-4). The superfluid behavior is now understood to be a manifestation of Bose–Einstein condensation, which occurs only with collections of bosons.
It is theorized that at 0.2 K and 50 atm, solid helium-4 may be a superglass (an amorphous solid exhibiting superfluidity).[1][2][3]
Helium-4 also exists on the Moon and—as on Earth—it is the most abundant helium isotope.[citation needed]
The helium-4 atom[edit]
The helium atom is the second simplest atom (hydrogen is the simplest), but the extra electron introduces a third 'body', so the solution to its wave equation becomes a 'three-body problem', which has no analytic solution. However, numerical approximations of the equations of quantum mechanics have given a good estimate of the key atomic properties of helium-4, such as its size and ionization energy.
The size of the 4He nucleus has long been known to be in the order of magnitude of 1 fm. In an experiment involving the use of exotic helium atoms where an atomic electron was replaced by a muon, the nucleus size has been estimated to be 1.67824(83) fm.[4]
Stability of the 4He nucleus and electron shell[edit]
The nucleus of the helium-4 atom is identical to an alpha particle. High-energy electron-scattering experiments show its charge to decrease exponentially from a maximum at a central point, exactly as does the charge density of helium's own electron cloud. This symmetry reflects similar underlying physics: the pair of neutrons and the pair of protons in helium's nucleus obey the same quantum mechanical rules as do helium's pair of electrons (although the nuclear particles are subject to a different nuclear binding potential), so that all these fermions fully occupy 1s orbitals in pairs, none of them possessing orbital angular momentum, and each canceling the other's intrinsic spin. Adding another of any of these particles would require angular momentum, and would release substantially less energy (in fact, no nucleus with five nucleons is stable). This arrangement is thus energetically extremely stable for all these particles, and this stability accounts for many crucial facts regarding helium in nature.

For example, the stability and low energy of the electron cloud of helium causes helium's chemical inertness (the most extreme of all the elements), and also the lack of interaction of helium atoms with each other (producing the lowest melting and boiling points of all the elements).
In a similar way, the particular energetic stability of the helium-4 nucleus, produced by similar effects, accounts for the ease of helium-4 production in atomic reactions involving both heavy-particle emission and fusion. Some stable helium-3 is produced in fusion reactions from hydrogen, but it is a very small fraction, compared with the highly energetically favorable production of helium-4. The stability of helium-4 is the reason that hydrogen is converted to helium-4, and not deuterium (hydrogen-2) or helium-3 or other heavier elements during fusion reactions in the Sun. It is also partly responsible for the alpha particle being by far the most common type of baryonic particle to be ejected from an atomic nucleus; in other words, alpha decay is far more common than cluster decay.
1 Mole Of Gas
The unusual stability of the helium-4 nucleus is also important cosmologically. It explains the fact that, in the first few minutes after the Big Bang, as the 'soup' of free protons and neutrons which had initially been created in about a 6:1 ratio cooled to the point where nuclear binding was possible, almost all atomic nuclei to form were helium-4 nuclei. The binding of the nucleons in helium-4 is so tight that its production consumed nearly all the free neutrons in a few minutes, before they could beta decay, and left very few to form heavier atoms (especially lithium, beryllium, and boron). The energy of helium-4 nuclear binding per nucleon is stronger than in any of those elements (see nucleogenesis and binding energy), and thus no energetic 'drive' was available to make elements 3, 4, and 5 once helium had been formed. It is barely energetically favorable for helium to fuse into the next element with a higher energy per nucleon (carbon). However, due to the rarity of intermediate elements, and extreme instability of beryllium-8 (the product when two 4He nuclei fuse), this process needs three helium nuclei striking each other nearly simultaneously (see triple alpha process). There was thus no time for significant carbon to be formed in the few minutes after the Big Bang, before the early expanding universe cooled to the temperature and pressure where helium fusion to carbon was no longer possible. This left the early universe with a very similar hydrogen–helium ratio as is observed today (3 parts hydrogen to 1 part helium-4 by mass), with nearly all the neutrons in the universe trapped in helium-4.
All heavier elements—including those necessary for rocky planets like the Earth, and for carbon-based or other life—thus had to be produced, since the Big Bang, in stars which were hot enough to fuse elements heavier than hydrogen. All elements other than hydrogen and helium today account for only 2% of the mass of atomic matter in the universe. Helium-4, by contrast, makes up about 23% of the universe's ordinary matter—nearly all the ordinary matter that is not hydrogen (1H).
Mass Of 1 Mole Of Electrons
See also[edit]
References[edit]
- ^Giulio Biroli; Claudio Chamon; Francesco Zamponi (2008). 'Theory of the superglass phase'. Physical Review B. 78 (22): 19. arXiv:0807.2458. Bibcode:2008PhRvB..78v4306B. doi:10.1103/PhysRevB.78.224306.
- ^'Press release: Supersolid or superglass? Cornell researchers study a strange state of matter in helium - Cornell Chronicle'.
- ^Yu, Xiaoquan; Mueller, Markus (2011). 'Mean field theory of superglasses'. Physical Review B. 85 (10): 104205. arXiv:1111.5956. Bibcode:2012PhRvB..85j4205Y. doi:10.1103/PhysRevB.85.104205.
- ^Julian J. Krauth; Schuhmann, Karsten; Ahmed, Marwan Abdou; et al. (2021). 'Measuring the α-particle charge radius with muonic helium-4 ions'. Nature. 589 (7843): 527. doi:10.1038/s41586-021-03183-1.
External links[edit]
- Tur, Clarisse (2009), 'DEPENDENCE OF s-PROCESS NUCLEOSYNTHESIS IN MASSIVE STARS ON TRIPLE-ALPHA AND 12
C
(α, γ)16
O
REACTION RATE UNCERTAINTIES', The Astrophysical Journal, 702, arXiv:0809.0291, Bibcode:2009ApJ...702.1068T, doi:10.1088/0004-637x/702/2/1068
| Lighter: helium-3 | Helium-4 is an isotope of helium | Heavier: helium-5 |
| Decay product of: lithium-5(p) helium-5(n) beryllium-6(2p) beryllium-8(α) | Decay chain of helium-4 | Decays to: Stable |